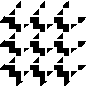Annual DIMACS REU graph puzzle

Every year we create a network with all the REU students and their mentors. The rule used to create the specific network configuration is given to the REU students as a puzzle to solve on picture day. The winner receives a small prize and a mention on this webpage!

Winners!

2018: Scott Harman
2017: Jakub Pekarek
2016: Thomas Murrills

2018 - 3rd annual DIMACS REU graph puzzle

Solution:
Each student is assigned two variables, r and θ, which correspond to the polar coordinates on a plane:
r = Number of letters in student's last name
θ = (Position in the alphabet of the first letter of the first name)*360/26
[i.e. A=0 degrees, B=1*360/26=13.84 degrees, ... , Z=25*360/26=346.15 degrees.]
Connect two students if their Euclidean distance is smaller than 4.
Mentors are simply connected to the students they supervised.

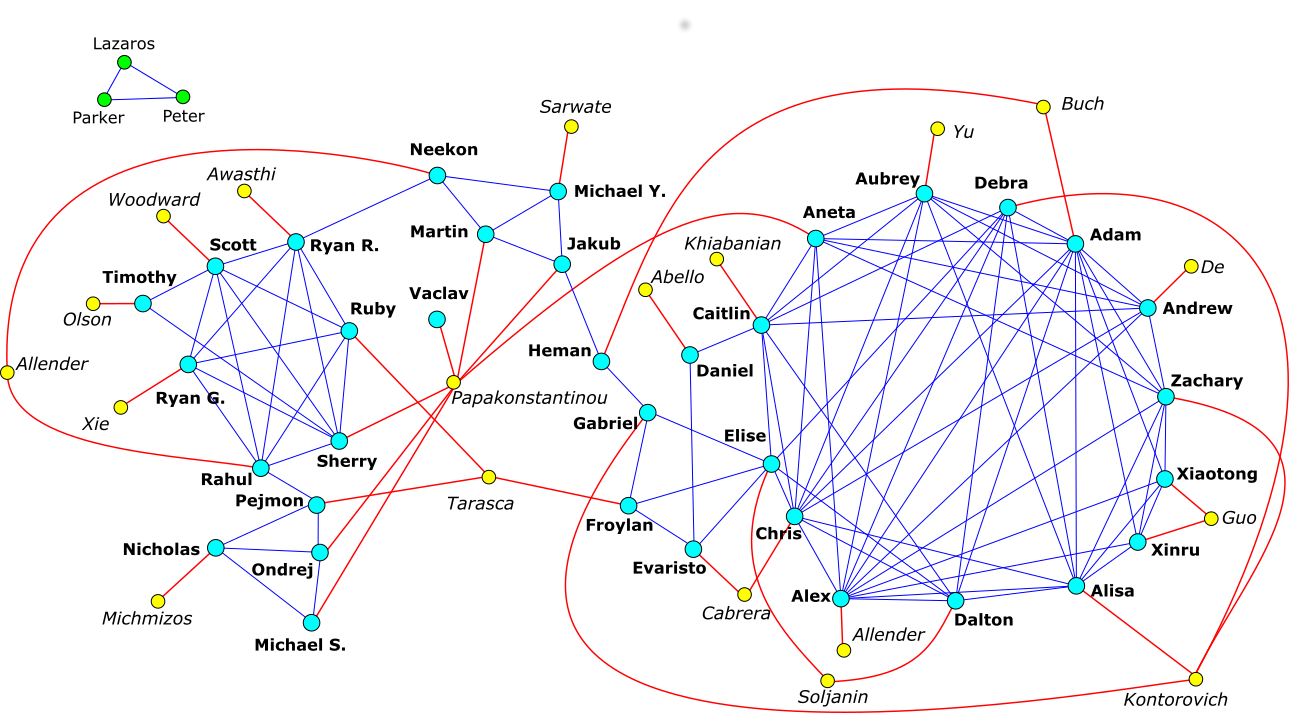
2017 - 2nd annual DIMACS REU graph puzzle

Solution:
Call L_name the distance in the alphabet between the two first letters in a student's first name
(for example, Aaron has L_name=0 and Edgar has L_name=1).
Connect two students with a thick line if they have the same L_name value
and connect them with a thin line if the difference of their L_name values is 1.
Mentors are simply connected to the students they supervised.

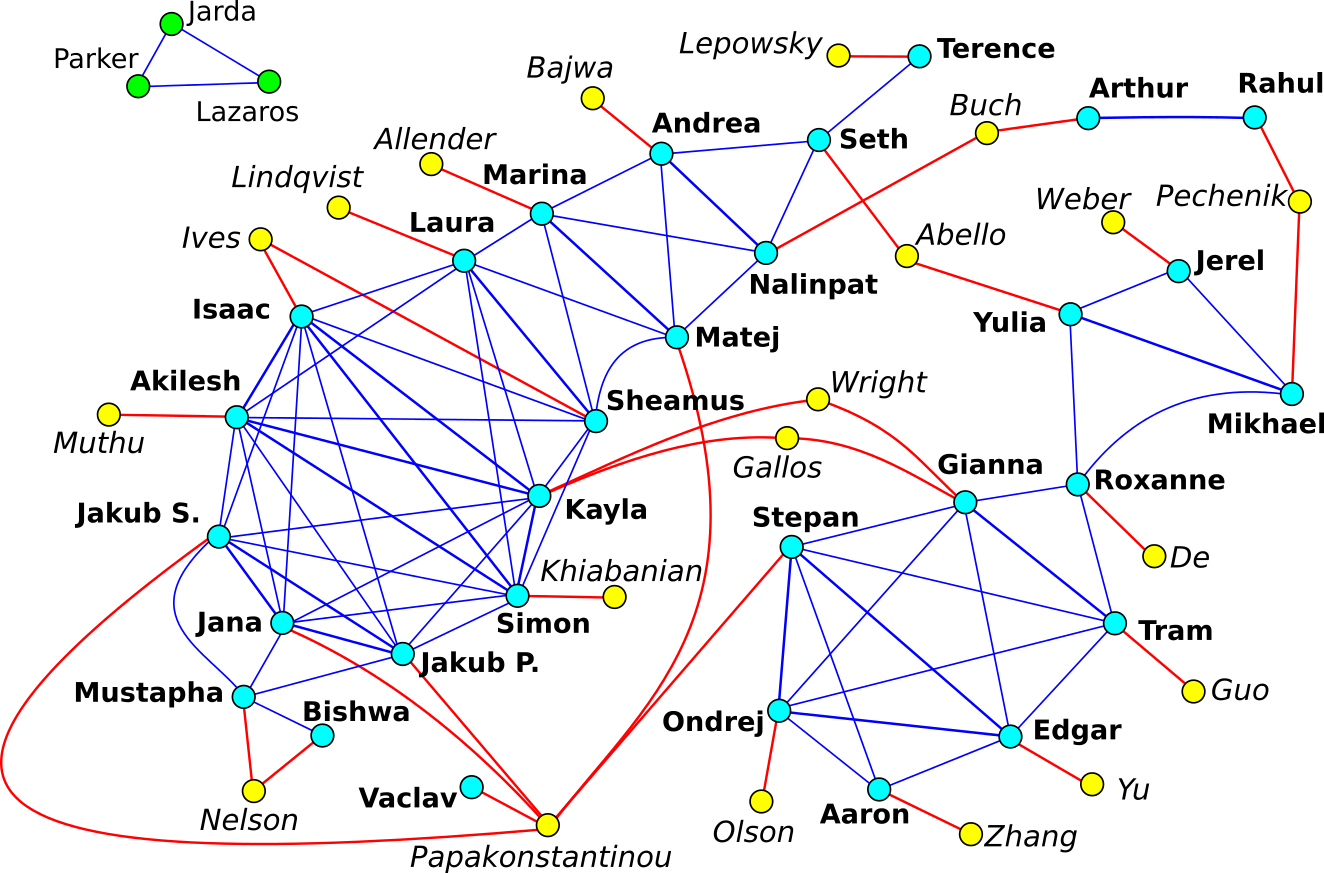
2016 - 1st annual DIMACS REU graph puzzle

Solution:
Map each node to a point (x,y) in a Euclidean plane where
x=number of letters in student's first name
y=number of letters in student's last name
Any two points within distance 1 are then connected in the graph.
Mentors are simply connected to the students they supervised.